Our Deconvolution Tool
Our Demo
Here is a link to the MATLAB code. Check the README for more detailed usage instructions.
Here is an example audio file that has been run through our finished demo:
Here are some more sample outputs of our final deconvolution tool, along with time- and frequency-domain graphs:
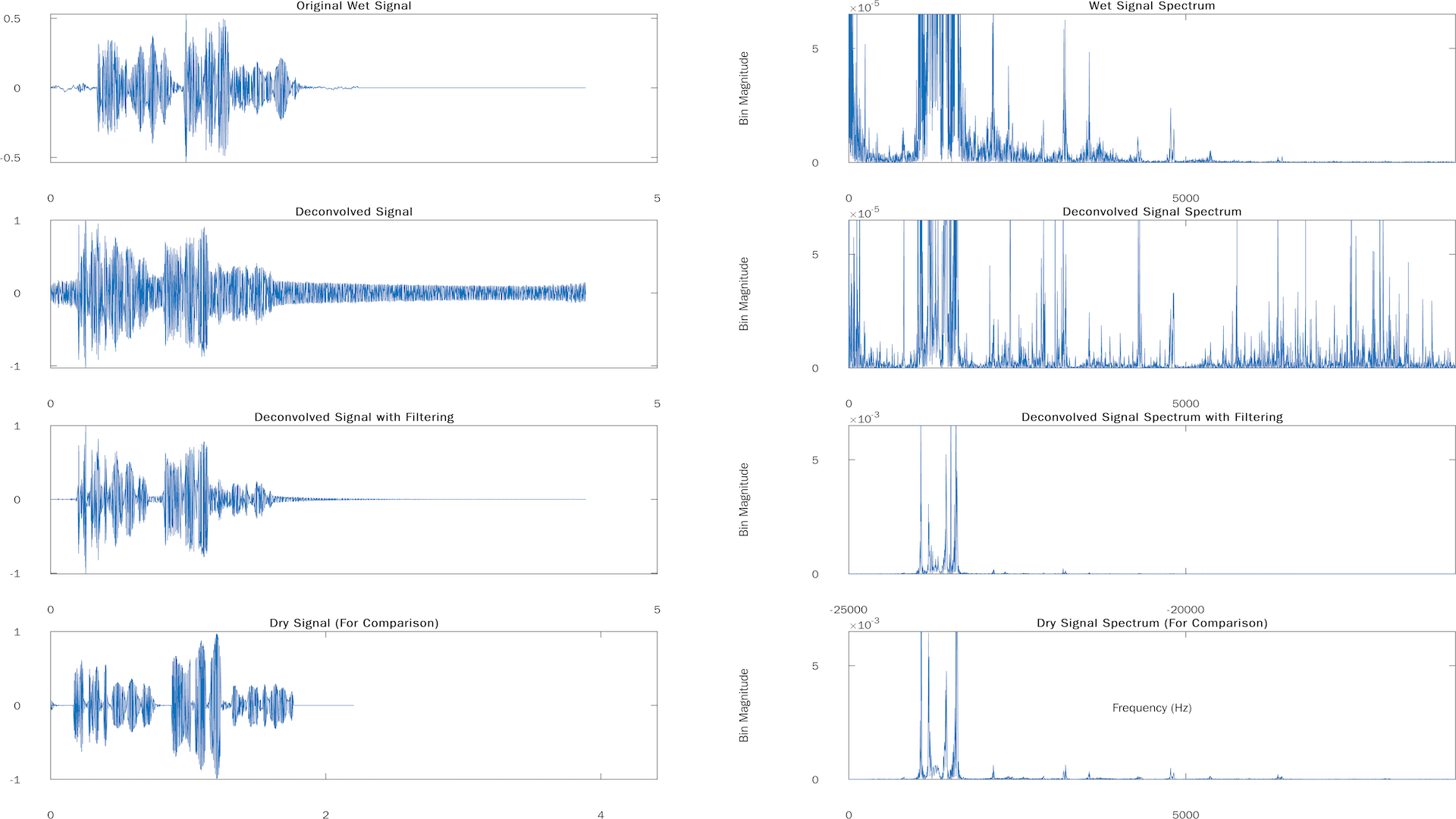
Flute Sample
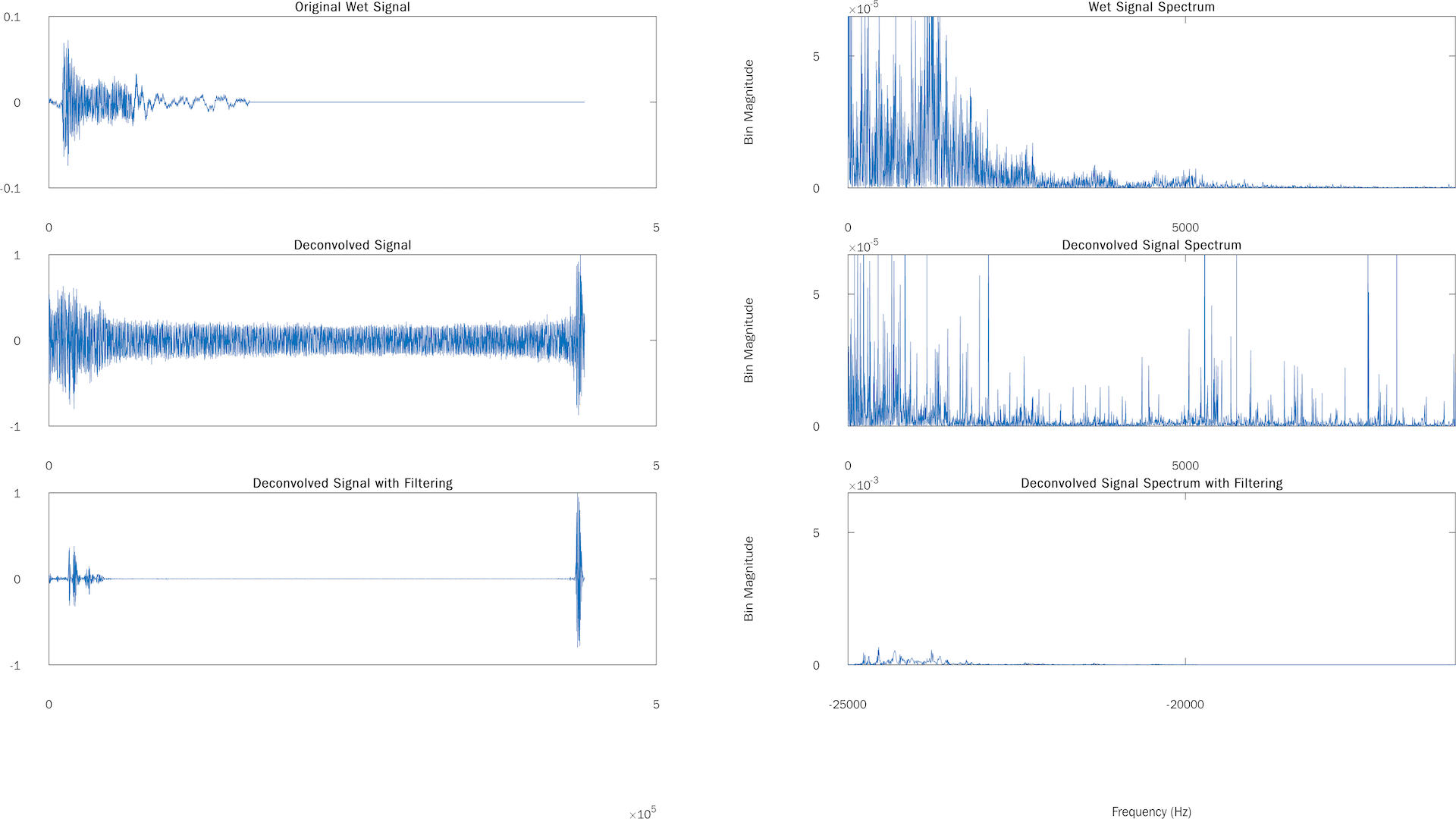
Speech Sample
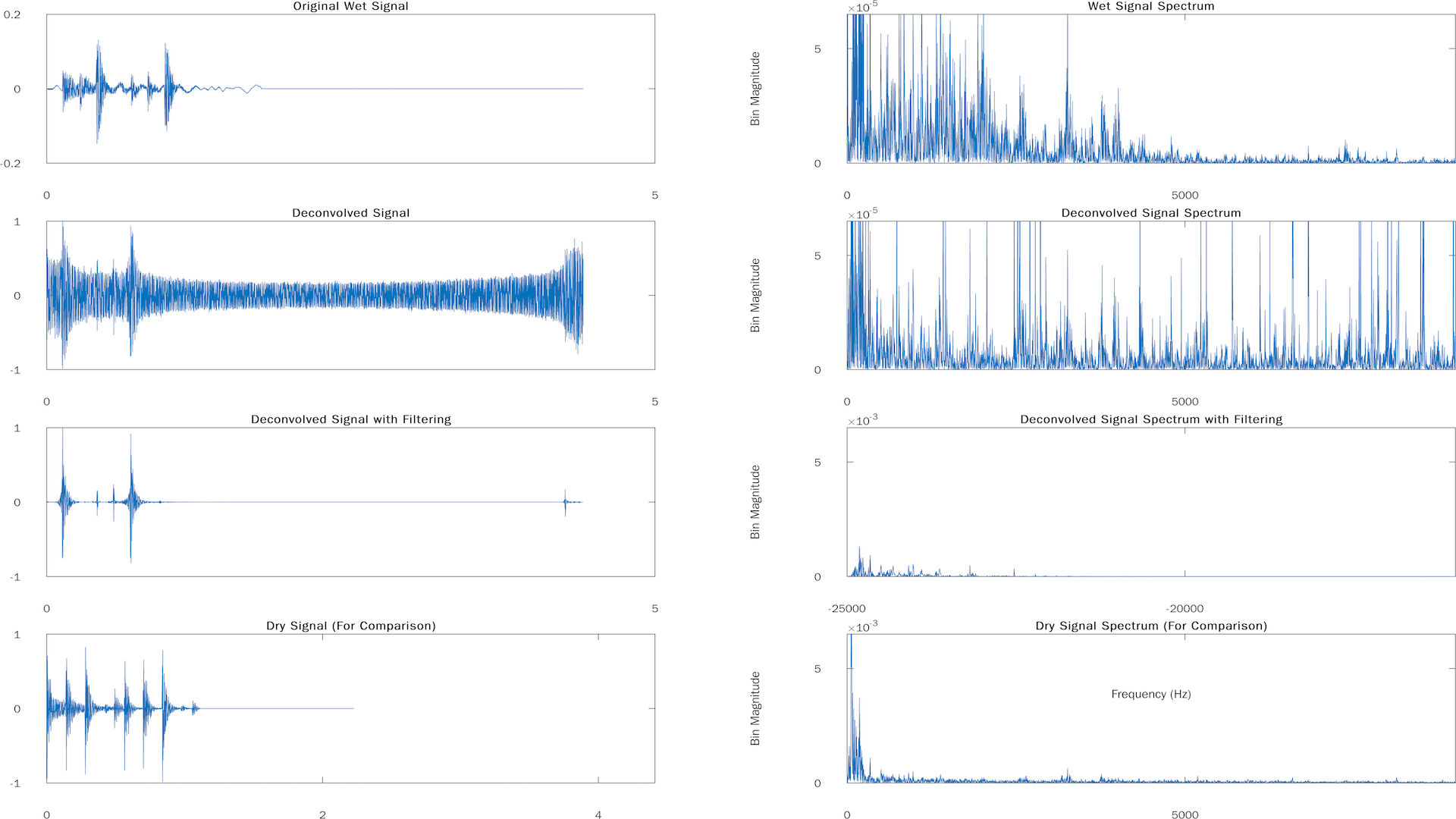
Drums Sample
Cello Sample
First Attempts at Deconvolution
To start, we used more obviously reverberant inputs: for example, a drum sample convolved with an IR recording of a church to test our code. The first test was to convolve the drums with the church IR, and then immediately deconvolve that convolved signal. First, we tried using MATLAB’s deconv() function but ran into difficulties running it with audio. So, we instead decided to try manually deconvolving by dividing the output by the impulse response in the frequency domain. However, this caused the amplitude of the deconvolved signal to blow up to very large numbers, producing a short glitch sound. We later realized that this was a result of dividing by zeros and small values in the frequency domain. We corrected this by replacing 0s with insignificant 1*10^-n values and ultimately chose to implement deconvolution as division in the frequency domain. The results of this were far from perfect, and though differences could be seen in the graphs, the deconvoluted “dry” signal sounded more like a distorted version of the convolved signal than the original dry drum loop. These unexpected hiccups in direct deconvolution made us realize we need to spend more time improving our Deconvolution tool before looking into Blind Deconvolution.
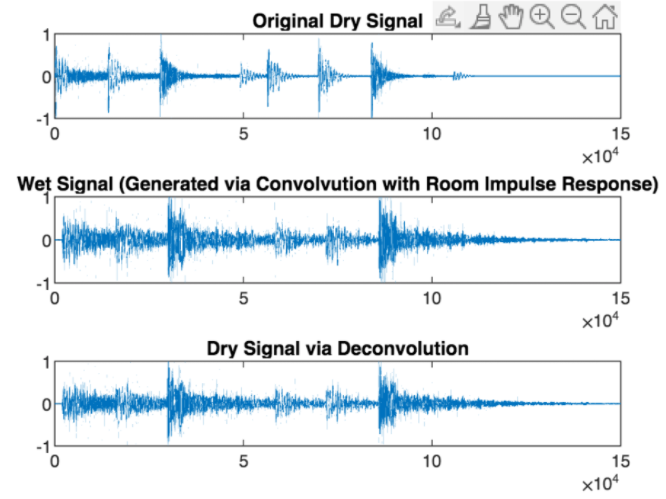Direct Deconvolution in Time
Improving Our Algorithm
The next step was to improve our deconvolution algorithm by testing it on our real-world IR and wet recordings. From our previous work, we knew this was unlikely to work perfectly due to the nonlinearities present in the real-world IR capture process. One of these confounding variables is the fact that the microphone on our recorder imperfectly captures the IR due to noise, the frequency spectral sensitivity of the microphone design, and response of the room at the microphone position. Still, we wanted to see what the results would be and whether our recordings would be adequate for future use. Instead of testing all 16 recordings, we selected 4 (enough to cover every room and source sound once). These combinations were chosen somewhat arbitrarily, as we reasoned that it was most important to get a quick overview of what each space was doing and whether each instrument was usable. The combinations were:
-
Drums + Jazz Room
Cello + Elevator Room
Flute + Band Room
Speech + Lobby
Each deconvolved clip generated in this way had significant audible artifacts. Most notably, each audio file had multiple ringing resonances at a variety of frequencies creating an unpleasant “metallic” sound as a result of the deconvolution algorithm. Attempts to eliminate this through bandpass filtering to inputs only lead to a bandpassed output and did not remove the resonances in the pass band.
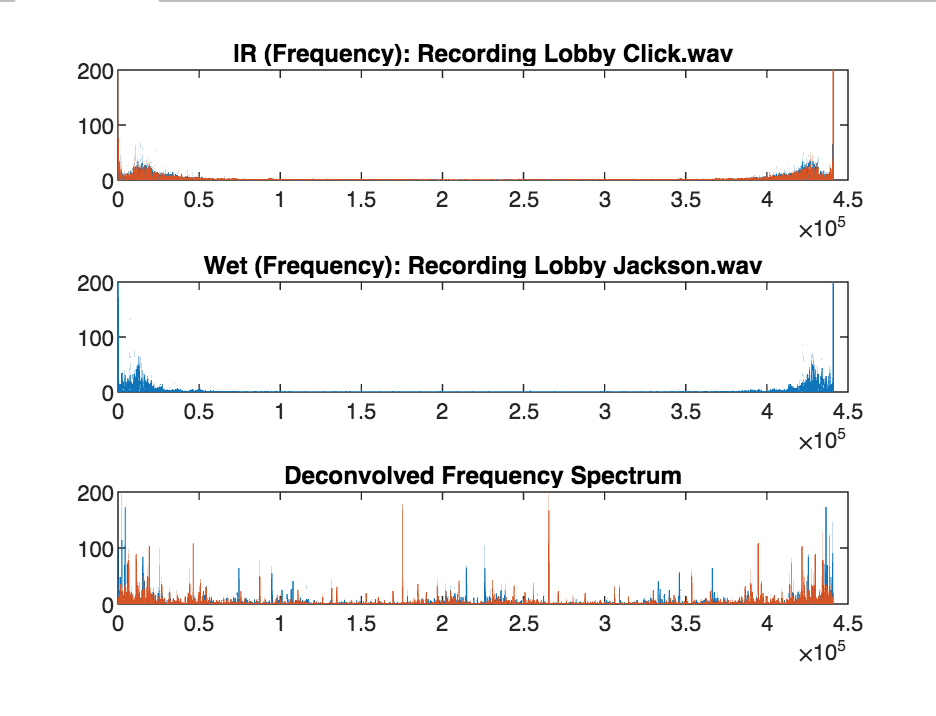Figure 1: Frequency analysis for the lobby speech recording. The unpleasant resonances are clearly visible in the deconvolved graph and are caused by small values in the denominator (the IR’s frequency spectrum).
Additionally, several clips had a sort of “reverse reverb” artifact where the reverberant sound would swell into the transients. This was particularly noticeable with the drums and the flute. Finally, several of the clips were rearranged in time. For example, the speech sample which initially said “I’m sitting in a room” was rearranged to be “sitting in a room… …I’m”. This happened because the IR recordings we were inputting had pauses before and after the click rather than just starting off with the click.
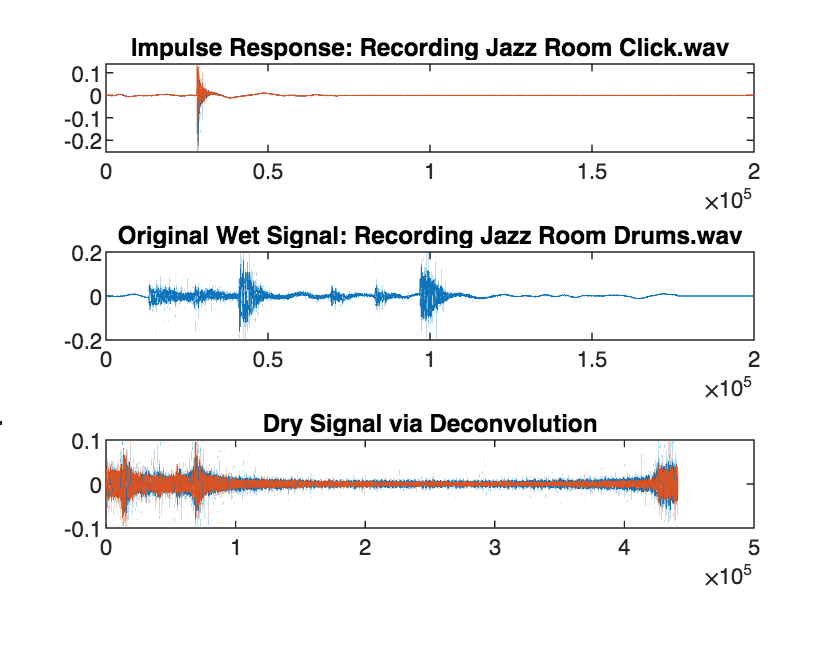Figure 2: Time-domain graphs of the drum recording in the jazz room. Both the “reverse reverb” and rearrangement artifacts are visible in the deconvolved signal. (Note that the scale for the deconvolved signal has been adjusted to show the full waveform).
Interestingly, it appears that our earlier hypothesis of deconvolution eliminating the filtering caused by the speaker was confirmed. This is most notable when examining the high frequencies. The AN-X1000+ monitors produced noticeably less high frequency content on site (and in our recordings), yet in these deconvolved files, this high end detail was actually restored. This was especially noticeable with the cello recording, as the high end bow noise is audible in the original sample and deconvolved file but is obscured in each room recording.
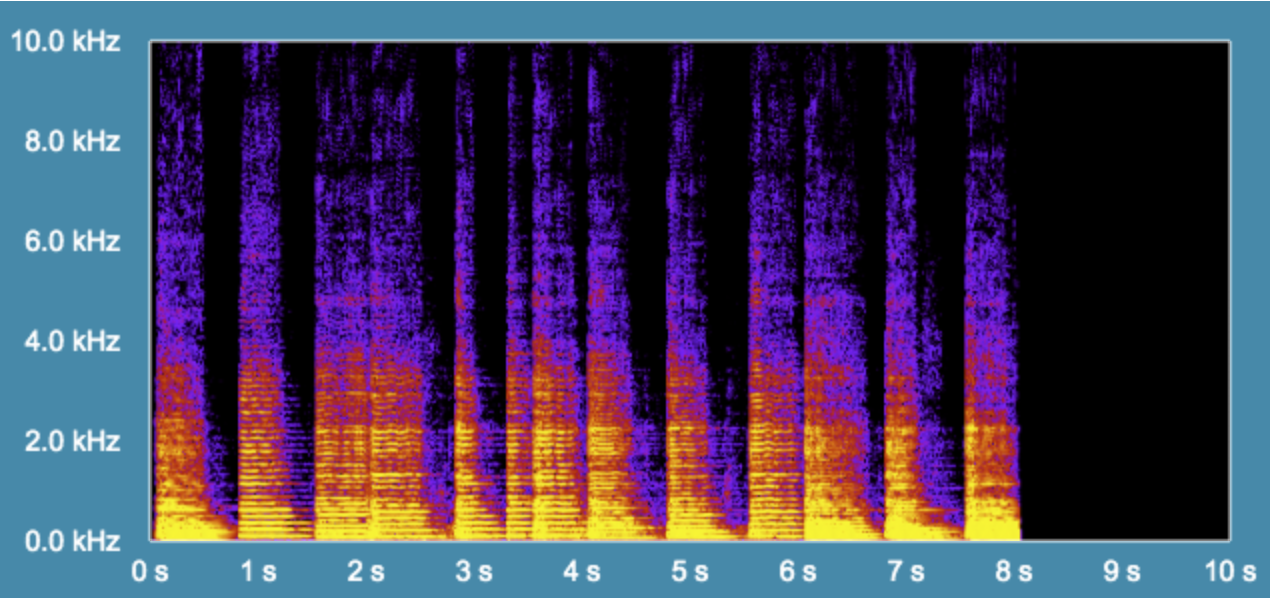Figure 3a: Spectrogram of the original cello sample. This spectrogram was generated using this online tool
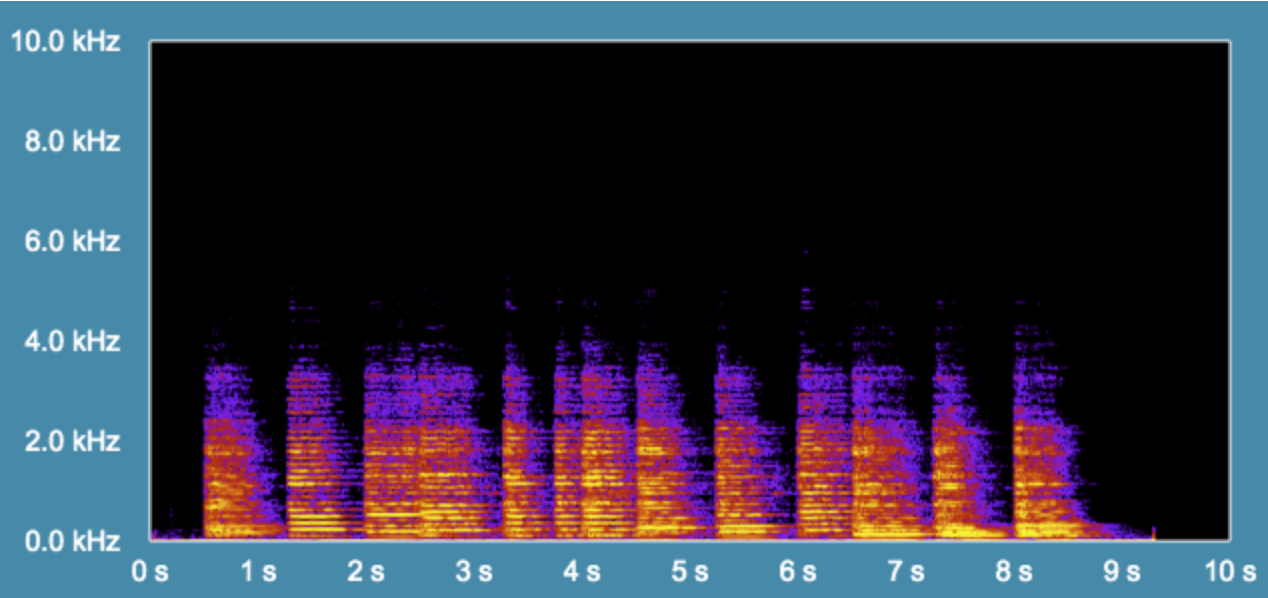Figure 3b: Time-domain graphs of the drum recording in the jazz room. Both the “reverse reverb” and rearrangement artifacts are visible in the deconvolved signal. (Note that the scale for the deconvolved signal has been adjusted to show the full waveform).
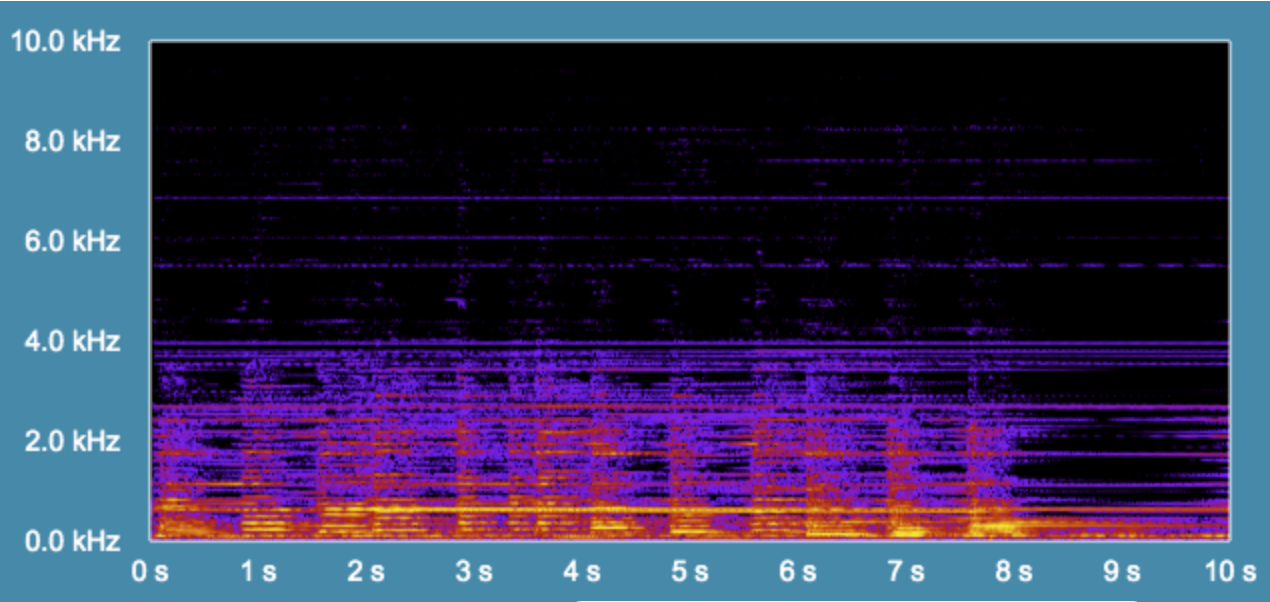Figure 3c: Spectrogram of the deconvolved elevator room cello recording. The ringing artifacts are clearly visible. Notice however, that some of the high frequencies have returned (note that the overall level of this audio file is quieter than the original).
Overall, our goal with running these recordings through our known deconvolution code was not to produce clean results, but to gain insight into potential challenges our blind deconvolution algorithm might face. Though in some cases, known deconvolution did help to reduce the reverb (it arguably improved the intelligibility of the speech+ lobby recording), the ringing artifacts present a major obstacle and will need to be addressed. The next step is to carefully analyze the inputs and outputs of these experiments and determine if any input features can be correlated with these resonances. Research into existing methods of solving this problem will also be needed.
Our Final Deconvolution Algorithm
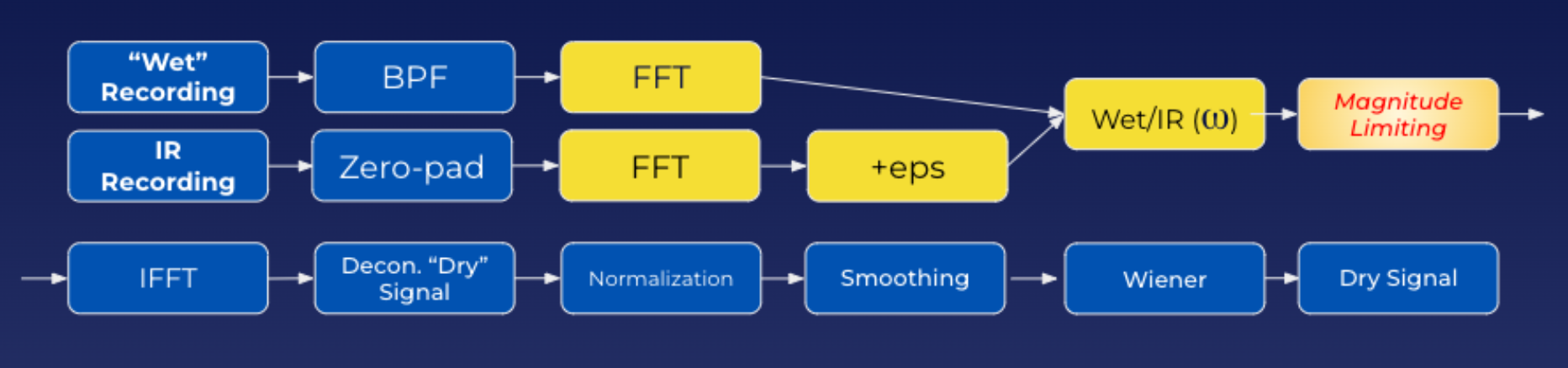Signal Chain Block Diagram
We were able to design a deconvolution tool which mitigated the noise introduced by processing real world recordings. This was achieved through a multi-stage design seen in the block diagram above. Some of the key components of the design are the initial Band Pass filter applied to the wet recording before FFT, the insignificant value added to the denominator +eps, and the smoothing applied after deconvolution.
As an example, for the recorded voice source signal, we decided to place the cutoffs at 200 and 9000 Hz. These choices preserve the most important frequency information in the voice for intelligibility (2000-9000Hz) and tone (200-500Hz). Since the frequency magnitudes outside the passband are limited, this prevents those frequencies from multiplying with the impulse response frequencies and producing a noisy output.
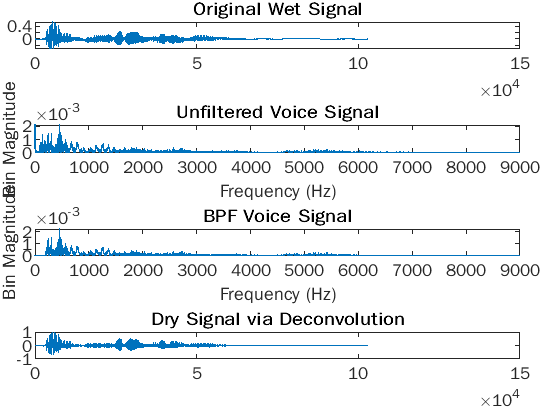Bandpass-filtered voice signal
We are using a general purpose signal smoothing algorithm from Professor Tom O’Haver (2). The smoothing algorithm works similarly to a moving average filter, wherein the smoothing is applied over a window of samples of the signal and averages the values within the window to prevent samples from being significantly higher than their neighbors. A rectangular window is the most simple form, since it simply averages the window (Figure 4). However, it is conventional to shape the smoothing window by weighting the values across the window. This is called changing the window shape: Figure 5 shows triangular smoothing for a 5 sample window.
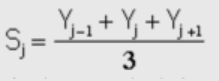Figure 4 (2)
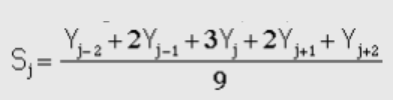Figure 5 (2)
By applying the smoothing algorithm at the end of our process, we are reducing the amount of high frequency noise introduced by the tool. This leaves the higher-magnitude, lower frequencies which are more likely to be important to the content of the dry signal. This effectively serves as a low pass filter.
The final stage of our process is a Wiener filter. The Wiener filter is a method of cleaning up a noisy signal by minimizing the mean square error in the frequency domain between it and some assumed output. For the purposes of our project, we used a noise reduction Matlab function which we obtained online (3).
This function was highly effective at removing the noise introduced by deconvolution, but did introduce some artifacts of its own (most notably warbling “birdies”). Since this function was designed for speech, its effectiveness varied and we decided to include it as a toggleable option. In the future, one step we could take would be to design our own denoising function so that its intensity and assumed output could be adjusted depending on the situation.
Frequency Magnitude Limiting
One initially promising denoising method we were using was Frequency Magnitude Limiting. Its place in the block diagram is highlighted in red. This was a crude frequency domain operation which limited the magnitude of any frequencies which exceeded that threshold. This was possible because the ringing which resulted from direct deconvolution was often greater in magnitude than the frequency content of the desired dry signal, so by clipping the ringing magnitudes to be roughly equivalent with the maximum magnitude of the source signal, the effects of the ringing were less apparent. This is true at least spectrally, as the frequency domain plots with magnitude limiting looked nearly identical to the original dry frequency spectrums, which was our goal.
However, in the time domain and aurally, there were still a lot of issues. The ringing would remain during silent periods of the signal, since those frequencies were held constant. Additionally, we would have to manually set the threshold for the limiting. Upon reflection, it would be possible in the future to find a metric for the average magnitude of the frequency spectrum of the dry signal, then limit all frequency magnitudes above that threshold so it could be set dynamically. We decided to remove this process from our tool because it was not flexible to different types of sources.
Minor Speed Optimization
Early on in this project, we struggled to process long, high-sample-rate audio files with the fft and ifft functions. There's a lot of individual data points, and despite the fact that those functions are run on multiple CPU cores at once by default in MATLAB, it was still taking a considerable time to process. As a minor optimization step, we convert the MATLAB arrays representing our input sample to "gpuArrays," which, if the user has a MATLAB-compatible GPU, will ensure those cost-intensive functions run on the GPU rather than the CPU. This should save a variable (but non-zero) amount of processing time, depending on the strength of the GPUs and CPUs in question.